机械优化问题

2022-06-16 Comments

带约束的多元函数最小值。

1、Fmincon函数求解多元函数的最小值

求函数 $ e^{(x+y)^2}+(x-1)^2 $的最小值。

已知：

$St.\begin{cases} x+y\ge1 \\x+2y=1.5 \\ x\ge0.6\\x\ge0\\ y\ge0\\z\ge0 \end{cases}$

1、尝试在无约束条件下求解全局最小值：

fun=@(x,y)exp((x+y).^2)+(x-1).^2
objfun=@(x)fun(x(1),x(2));
x0=[0,0];
[x,fval]=fminsearch(objfun,x0)

2、尝试在有约束条件下求解局部最小值：

clear;clc
fun=@(x,y)exp((x+y).^2)+(x-1).^2
objfun=@(x)fun(x(1),x(2));
x0=[0,0];
A=[-1 -1];
a=-1;
Aeq=[1,2];
beq=1.5;
lb=[0.6 -inf];
ub=[];

[X,Fval]=fmincon(objfun,x0,A,a,Aeq,beq,lb,ub)

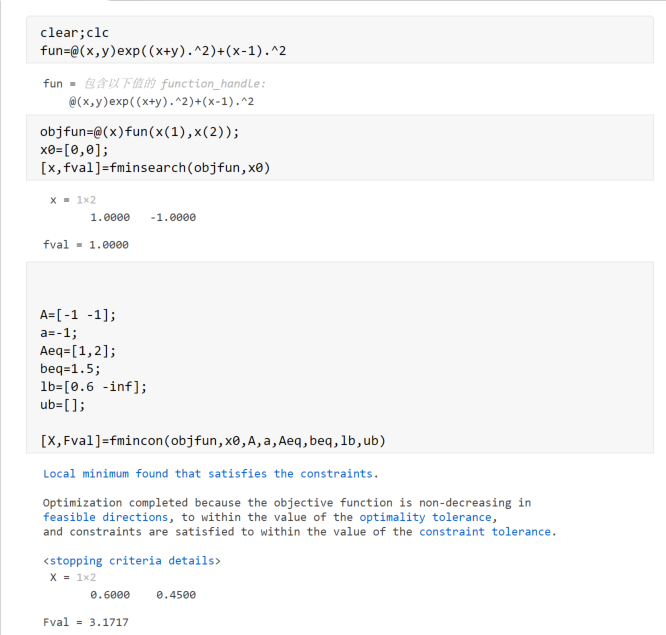
3、定义函数求解局部最小值最小值。

clear;clc
fun=@(x,y)exp((x+y).^2)+(x-1).^2
objfun=@(x)fun(x(1),x(2));
x0=[0,0];

A=[];%不等式约束系数
a=[];%不等式约束常数
Aeq=[];%等式约束系数
beq=[];%等式约束常数
lb=[];%下限
ub=[];%上限


[x,fval]=fmincon(objfun,x0,A,a,Aeq,beq,lb,ub,@confun)

function [c ceq]=confun(x)
c=-x(1).^2-x(2).^2+1;
ceq=x(1).^2+2*x(2).^2-1.5;
end

1	opts=optimset('algorithm','sqp')%更换求解算法

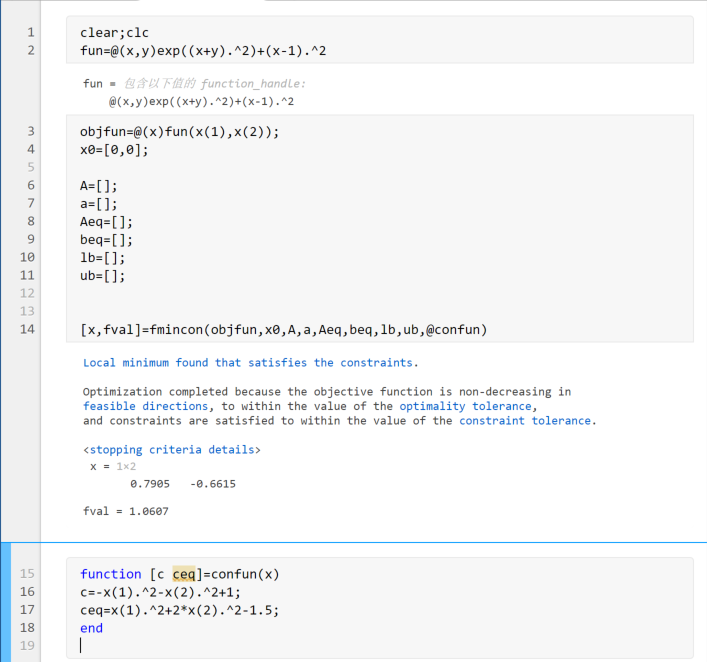
4、求解最小值一般步骤

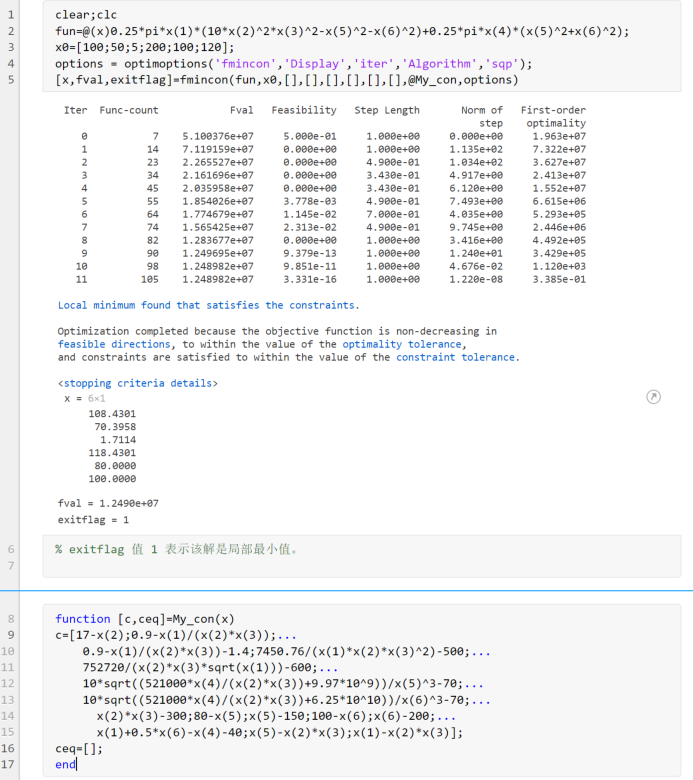
clear;clc
fun=@(x)0.25*pi*x(1)*(10*x(2)^2*x(3)^2-x(5)^2-x(6)^2)+0.25*pi*x(4)*(x(5)^2+x(6)^2);
x0=[100;50;5;200;100;120];
options = optimoptions('fmincon','Display','iter','Algorithm','sqp');
[x,fval,exitflag]=fmincon(fun,x0,[],[],[],[],[],[],@My_con,options)

function [c,ceq]=My_con(x)
    c=[17-x(2);0.9-x(1)/(x(2)*x(3));...
    0.9-x(1)/(x(2)*x(3))-1.4;7450.76/(x(1)*x(2)*x(3)^2)-500;...
    752720/(x(2)*x(3)*sqrt(x(1)))-600;...
    10*sqrt((521000*x(4)/(x(2)*x(3))+9.97*10^9))/x(5)^3-70;...
    10*sqrt((521000*x(4)/(x(2)*x(3))+6.25*10^10))/x(6)^3-70;...
    x(2)*x(3)-300;80-x(5);x(5)-150;100-x(6);x(6)-200;...
    x(1)+0.5*x(6)-x(4)-40;x(5)-x(2)*x(3);x(1)-x(2)*x(3)];
    ceq=[];
end

定义函数：fun=@(x)0.25*pi*x(1)*(10*x(2)^2*x(3)^2-x(5)^2-x(6)^2)+0.25*pi*x(4)*(x(5)^2+x(6)^2);
确定初始值：x0=[100;50;5;200;100;120];
编写求解器：[x,fval,exitflag]=fmincon(fun,x0,[],[],[],[],[],[],@My_con)
编写约束函数：My_con

5、运算过程

2、用遗传算法求解(GA)

1、遗传算法调用方式：

fun:定义为待求解函数
nvars:定义为变量数目
A:定义为非线性约束系数
b:定义为：非线性约束常数
Aeq：定义为线性约束系数
beq:定义为线性约束常数
lb:定义为自变量下限约束
ub:定义为自变量上限约束

2、调用GA求解问题

例子：

$min f(x)=p_1x_1^2+x_2^2-x_1x_2-2x_1-p_2x_2$

约束：

$St.\begin{cases} x+y\le2 \\-x_1+2x_2=2 \\ 2x_1+x_2\le3\\x_1\ge0\\ x_2\ge0 \end{cases}$

求解算法:

clear;clc
A = [1 1; -1 2; 2 1]; 
b=[2;2;3];
lb=zeros(2,1);
[x,fval,exitflag]=ga(@Myfun,2,A,b,[],[],lb)


function y=Myfun(x)
y=0.5*x(1)^2+x(2)^2-x(1)*x(2)-2*x(1)-6*x(2);
end

3、机械优化作业

1、第一二此作业主要采用fmincon函数和遗传算法

下面两道题分别采用了这两种算法，只需要修改我标注的需要修改的部分为题目要求即可完成运算。

代码：

clear;clc


%作业1
%%%%%%%%%%修改中间部分%%%%%%%%%%
homework1=@(x)100*(x(2)-x(1)^2)+(1-x(1))^2
x0=[0 0];
%%%%%%%%%%修改中间部分%%%%%%%%%%
[X,Fval]=fmincon(homework1,x0,[],[],[],[],[],[],@work1)
%%%%%遗传算法区块，不用删掉%%%%
E=[];
for i=1:20
    [x,fval]=ga(homework1,2,[],[],[],[],[],[],@work1);
    e=[i,x,fval];
    E=[E;e];
    
end
    E
%%%%%遗传算法区块，不用删掉%%%%

%% 作业2
%%%%%%%%%%修改中间部分%%%%%%%%%%
homework2=@(x)(x(1)-3)^2+x(2)^2
x0=[1,1];
lb=[0 0];
%%%%%%%%%%修改中间部分%%%%%%%%%%
[x,fval]=fmincon(homework2,x0,[],[],[],[],lb,[],@work2)
%%%%%遗传算法区块，不用删掉%%%%
E=[];
for i=1:20
    [x,fval]=ga(homework2,2,[],[],[],[],[],[],@work2);
    e=[i,x,fval];
    E=[E;e];
end
    E
%%%%%遗传算法区块，不用删掉%%%%

function [c,ceq]=work1(x)
%%%%%%%%%%修改中间部分%%%%%%%%%%
    c(1)=x(1)^2/9+x(2)^2/4-1;
    c(2)=x(1)^2-x(2)^2-1;
    ceq=[];
%%%%%%%%%%修改中间部分%%%%%%%%%%
end

function [ceq,c]=work2(x)
%%%%%%%%%%修改中间部分%%%%%%%%%%
    ceq=x(2)^2+x(1)^2-4;
    c=[];
%%%%%%%%%%修改中间部分%%%%%%%%%%
end

结果：

2、黄金搜索法

修改我标注修改的部分即可完成任务。

Homework 4

The objective function is $f(x)=x_2-7x+10$ ，Suppose the initial value are $x_0=0$,$h_0=1$, allowable error is $eps=0.01$;

Find the interval that contains the minimum.
Use the Golden search method and Quadratic interpolation method and Newton method, to find the optimal solution.

clear;clc

%%%%%%%%%%修改中间部分%%%%%%%%%%
x1=0; h1=1;epsilan=0.01;
%%%%%%%%%%修改中间部分%%%%%%%%%%
[a,b]=Forward_and_backward_Method(x1,h1);
x1=a+0.382*(b-a);y1=fx(x1);
x2=a+0.618*(b-a);y2=fx(x2);
    while abs(b-a)>epsilan
        if y1>y2
            a=x1;x1=x2;y1=y2;
            x2=a+0.618*(b-a);y2=fx(x2);
        else
            b=x2;x2=x1;y2=y1;
            x1=a+0.382*(b-a);y1=fx(x1);
       end
    end
xm=(a+b)/2;
['Optimal result:',blanks(3),'xm=[',num2str(xm),']',blanks(6),'fm=',num2str(fx(xm))]


function [a,b]=Forward_and_backward_Method(x0,h0)
    h=h0;x1=x0;y1=fx(x1);
    x2=x1+h;y2=fx(x2);
    if y2>y1
        h=-h;x3=x1;f3=y1;x1=x2;y1=y2;x2=x3;y2=f3;
    end
    x3=x2+h;f3=fx(x3);
    while y2>=f3
        x1=x2;y1=y2;x2=x3;y2=f3;
        x3=x2+2*h;f3=fx(x3);
    end
    if h<0
        a=x3;b=x1;
    else
        a=x1;b=x3;
    end
end
function f=fx(w)
    %%%%%%%%%%修改中间部分%%%%%%%%%%
    f=w^2-7*w+10;
    %%%%%%%%%%修改中间部分%%%%%%%%%%
end

3、牛顿法

clear;clc
syms x;
%%%%%%%%%%修改中间部分%%%%%%%%%%
f= x^2-7*x+10 ;
x0=0;epsilon=1e-2;
%%%%%%%%%%修改中间部分%%%%%%%%%%
[xm,f_val]=Newton_oneD_method (f,x0,epsilon);
['Optimal result:',blanks(3),'[xm   f_val]=[',...
    num2str(xm),blanks(6),num2str(f_val),']']

function [x_m,f_val]=Newton_oneD_method (f,x0,epsilon)
    syms x;
    f_d1=diff(f,x);% first  derivative of f
    f_d2=diff(f_d1,x);
    tol=1;i=0;
    while tol>epsilon 
        f_d1_x0=eval(subs(f_d1,x,x0));
        f_d2_x0=eval(subs(f_d2,x,x0));
    x1=x0-f_d1_x0/f_d2_x0;
    f1=eval(subs(f,x,x1));
    i=i+1;
    fprintf(1,' Number of Iterations:  i=% d , x=% 3.8f , f =% 3.8f\n',i,x1,f1)

    tol=abs(x1-x0);
    x0=x1;    
    % Anim_m(x0,x1,x2,g);
    end
    x_m=x0;f_val=eval(subs(f,x,x_m));
end

4、二次插值法

clear;clc
%%%%%%%%%%修改中间部分%%%%%%%%%%
f=@(x) x.^2-7*x+10 
epsilon=1e-2;x0=0;h0=1;
%%%%%%%%%%修改中间部分%%%%%%%%%%
[a,m,b]=Forward_and_backward_Method(f,x0,h0);
 x2=m;
 %x2=(a+b)/2;
x123=[a x2 b];
x=a:0.01:b;y=f(x);
plot(x,y);
[xm,f_val]=Quadratic_method(x123,f,epsilon);
if xm~=inf
['Optimal result:',blanks(3),'[xm,f_val]=[',...
    num2str(xm),blanks(6),num2str(f_val),']'];
else
    ['Fail to find the best result!'];
end


function [x_m,f_val]= Quadratic_method(x123,f,epsilon)
    x1 = x123(1);x2 = x123(2);x3 = x123(3);
    i=0;F1=f(x1);F2=f(x2);F3=f(x3);
    if (F2<F1)&&(F2<F3)     %F1>F2<F3
        A=2*((x2-x3)*F1+(x3-x1)*F2+(x1-x2)*F3);
        if A==0
            fprintf(1,'   x2         x2=% 3.4f\n',x2)
            fprintf(1,'   F2        F2=% 3.4f\n',F2)
            x_m=inf; f_val=inf;
        else 
            B=((x2^2-x3^2)*F1+(x3^2-x1^2)*F2+(x1^2-x2^2)*F3);
            xp=B/A;
            Fp=f(xp);
            while abs(xp-x2)>epsilon
                if (xp-x2)>0
                    if F2<Fp
                        x3=xp;F3=Fp;
                    else
                        x1=x2;x2=xp;F1=F2;F2=Fp;
                    end
                else
                    if Fp<F2
                        x3=x2;F3=F2;x2=xp;F2=Fp;
                    else
                        x1=xp;F1=Fp;
                    end
                end
                A=2*((x2-x3)*F1+(x3-x1)*F2+(x1-x2)*F3);
                B=((x2^2-x3^2)*F1+(x3^2-x1^2)*F2+(x1^2-x2^2)*F3);
                xp=B/A;
                Fp=f(xp);
                i=i+1;
                fprintf(1,' Number of Iterations:  i=% d , xp=% 3.8f , Fp =% 3.8f\n',i,xp,Fp)
            end
            if F2<Fp 
                x_m=x2; f_val=f(x2);
            else
                x_m=xp; f_val=Fp;
            end
            fprintf(1,' Optimal Results: xm=% 3.8f  f_val =% 3.8f\n',x_m,f_val)
        end
    else
        fprintf(1,'   x2 NOT FITABLE')
          x_m=inf; f_val=inf;
    end
end


function [a,m,b]=Forward_and_backward_Method(fx,x0,h0)
    h=h0;x1=x0;f1=fx(x1);
    x2=x1+h;f2=fx(x2);
    if f2>f1
        h=-h;
        x3=x1;f3=f1;
        x1=x2;f1=f2;
        x2=x3;f2=f3;
    end
        h=2*h;
        x3=x2+h;f3=fx(x3);
    while f2>=f3
        x1=x2;f1=f2;
        x2=x3;f2=f3;
        h=2*h;
        x3=x2+h;f3=fx(x3);
    end
    a=min([x3,x1]);b=max([x3,x1]);
    m=x2;
end

本文链接： http://tuoxiao.github.io/2022/06/16/Mathematical_modeling/fmincon8/

TuTo

天地与我并生，万物与我为一。