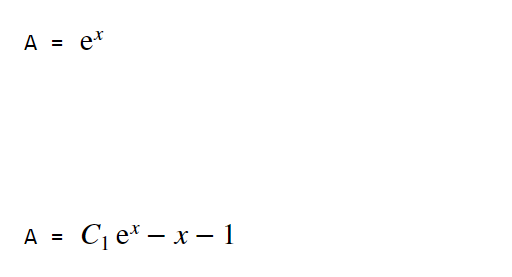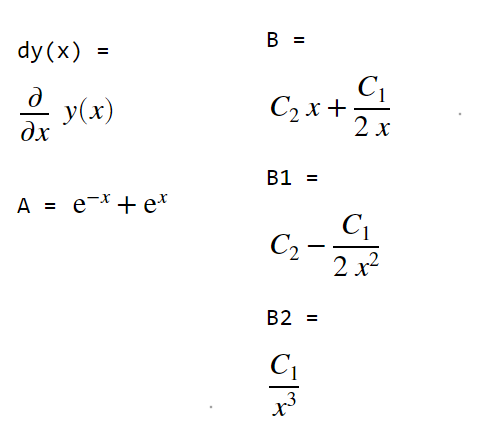Matlab微分方程

微分方程求解

一阶线性微分方程

• 形如 $y’+P(x)y=Q(x)$的函数称之为一阶线性常微分方程。其中：
  • $y’+P(x)y=0$，被称为 齐次微分方程。
  • $y’+P(x)y=Q(x)$，被称为 非齐次微分方程。

syms y(x)
ode=diff(y,x)-y==0;     %写出函数
cond=y(0)==1;           %定义初始条件
A=dsolve(ode,cond)


syms y(x)
ode=diff(y,x)-y==x;
cond=[];
A=dsolve(ode,cond)

• 结果
  

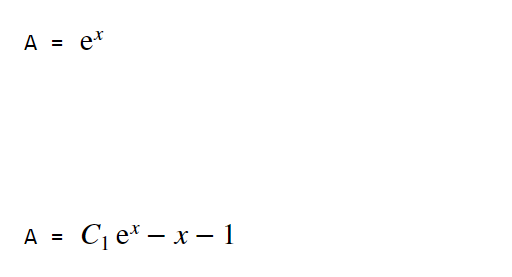
二阶微分方程

• 形如$y’’+py’+qy=f(x)$的方程被称为：二阶常系数微分方程

clear,clc,close all

syms y(x)
ode1=diff(y,x,2)-y==0;
dy=diff(y,x)
cond1=[y(0)==2,dy(0)==0];
A=dsolve(ode1,cond1)

syms y(x)
ode2=x^2*diff(y,x,2)+x*diff(y,x)-y==0;
cond2=[];
B=dsolve(ode2,cond2)
B1=diff(B,x)
B2=diff(B,x,2)

• 结果
  

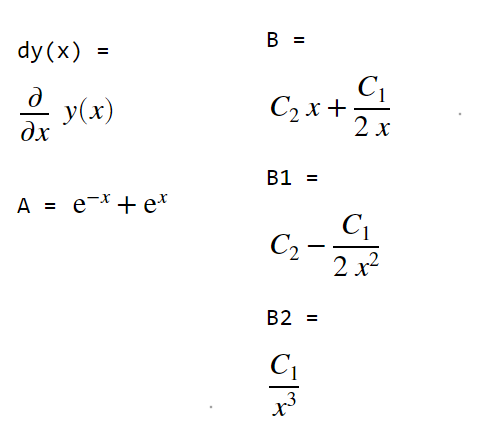
微分方程的数值解

  在工程和计算中常常需要求解微分方程，但微分方程的解析解通常很难得到，所以一种退而求其次的方法就是求其数值解。这里是使用Matlab中的ode45求解常微分方程数值解的简单说明。具体可使用”help ode45”命令查看它的帮助文档。

查看 Matlab Help 可以发现,ode45的用法如下：

[X,Y]=ode45(odefun,tspan,y0)

• 其中
  • odefun通常指方程所在函数函数名；
  • tspan通常指