目录
1 多项式及其函数1.1 多项式的创建与表达
· 输入多项式 $2x^4-85x^3+15x^2+100$1
a=ploy2sym([2 -85 15 100])
1.2 多项式的四则运算
1.2.1 加、减法
1 | a=[1 2 3 4 5]; |

1.2.2 乘法
1 | a=[1 2]; |
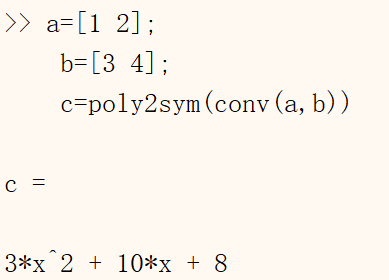
1.2.3 除法
1 | a=[1 4 9 15]; |
$[q,r]=deconv(b,a)$:
q为多项式b除以a的商户式;r为多项式b除以a的余式。返回的q,r仍为多项式系数向量。

1.3 多项式求导
k = polyder(p) : 求多项式p的导函数多项式。
k = polyder(a,b) : 求多项式a和b 乘积的导函数多项式。
[p,q] =polyder(a,b):求多项式b与多项式a相除的导函数多项式,导函数的分子存在p中,分母存在q中。其中,参数a,b是多项式的系数向量,返回结果p,q也是多项式的系数向量。
1 | a=[2 4 6 -8 10] |
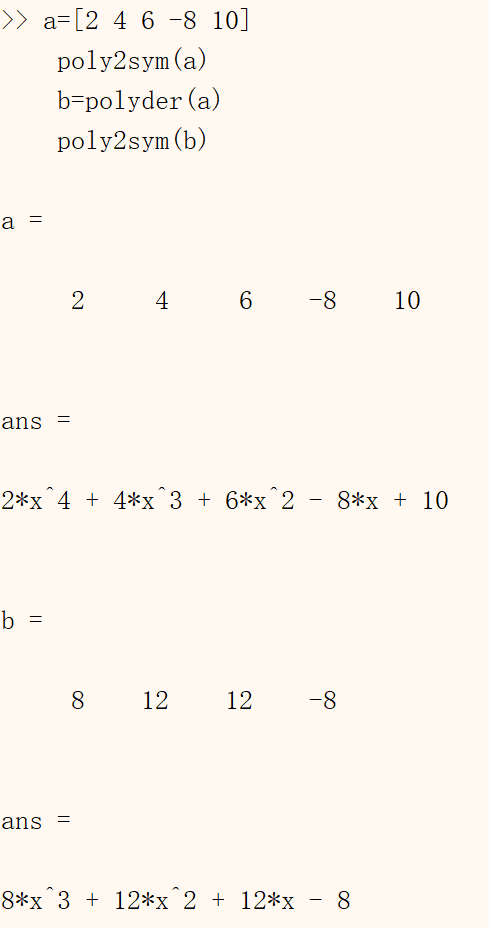
· 已知多项式$p(x)=2x^3-x^2+3$和$q(x)=2x=1$,求如下导数:$p’、(p·q)’、(p/q)’$。
1 | clear all; |

1.4 多项式求值
1.4.1 polyval函数
· 已知多项式 $x^4+6x^3-9$ ,分别取$x=1.3$和一个给定的矩阵2x3个元素为自变量,计算该多项式的值。
1 | clear all; |
· 调用此函数时,有两种形式:
$y=poluval(A,x)$ —其中x为单独的自变量
$y=poluval(A,B)$ —其中B为一个自变量矩阵
1.4.2 polyvalm函数
· 已知多项式 $p(x)=3^3-x^2+5$ ,求矩阵 A=$\begin{pmatrix} -1 & 2 \\ -2 & 1 \end{pmatrix}$ 的多项式的值。1
2
3
4
5clear all;
p=[3 -1 0 5];
x=[-1 2; -2 1];
polyval(p,x)
polyvalm(p,x)
1.5 多项式求根
· 已知多项式 $x^3-6x^2-72x-27$ 的根。1
2
3
4clear all;
p=[1 -6 -72 -27];
k=poly2sym(p)
r=roots(p)
· 若已知多项式的根,可以反求多项式1
2
3
4
5r=[2 5 8 7]; %已知根
p=poly(r) %反求多项式系数
k=poly2sym(p) %导出多项式
r=roots(p) %再次求出多项式的根验证正确性
· 注意有根才能求根!
1.6 部分分式展开
对有理多项式 $\frac{10(s+2)}{(s+1)(s+3)(s+4)}$ 进行展开1
2
3
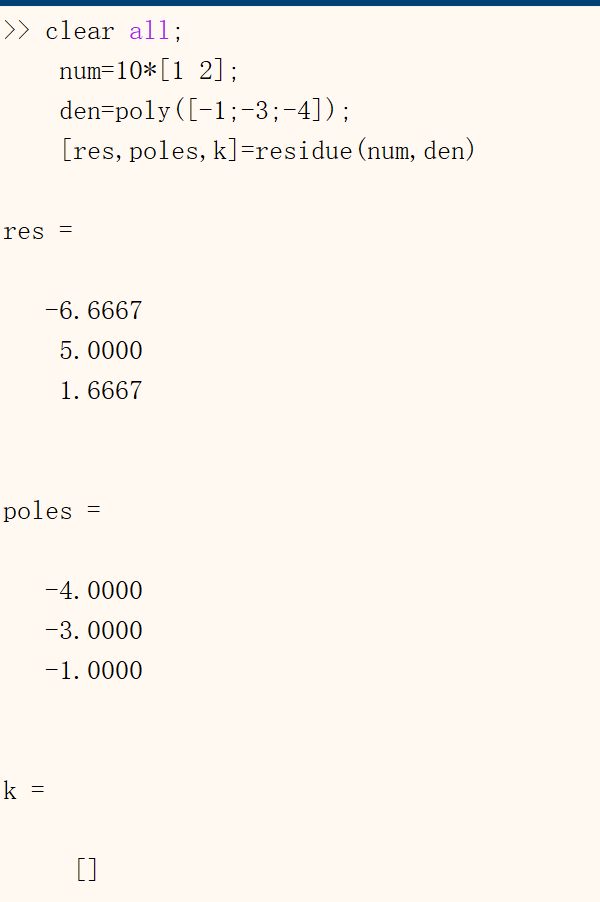
4clear all;
num=10*[1 2];
den=poly([-1;-3;-4]);
[res,poles,k]=residue(num,den)
结果是余数、极点和部分分式展开的常数项,如下:
$\frac{10(s+2)}{(s+1)(s+3)(s+3)}=\frac{-6.66667}{s+4}+\frac{5}{s+3}+\frac{1.6667}{s+1}$
1.7 求解线性方程组
方法一、
1 | a=[2 3 -1;8 2 3;45 3 9]; |
方法二:
1 | syms x y z |
1.8 解定积分
· 方法一:1
quad('x.*log(1+x)',0,1)
· 方法二:1
2syms x
int(x*log(1+x),0,1)
1.9 曲面拟合
最小二乘拟合
· 某地一煤矿,为估计其储量便于开采,先在该地进行开采,先在该地进行勘探。假设该地是一长方形区域,长为4km,宽为5km.勘探得到如下表所示数据:
| 编号 | 坐标/km | 煤层厚度/km | * | 编号 | 坐标/km | 煤层厚度/km |
|---|---|---|---|---|---|---|
| 1 | (1,1) | 13.2 | * | 11 | (3,1) | 23.28 |
| 2 | (1,2) | 25.80 | * | 12 | (3,2) | 26.48 |
| 3 | (1,3) | 8.47 | * | 13 | (3,3) | 29.14 |
| 4 | (1,4) | 25.27 | * | 14 | (3,4) | 12.04 |
| 5 | (1,5) | 22.32 | * | 15 | (3,5) | 14.58 |
| 6 | (2,1) | 15.47 | * | 16 | (4,1) | 19.95 |
| 7 | (2,2) | 21.33 | * | 17 | (4,2) | 23.73 |
| 8 | (2,3) | 14.49 | * | 18 | (4,3) | 15.35 |
| 9 | (2,4) | 24.83 | * | 19 | (4,4) | 18.01 |
| 10 | (2,5) | 26.19 | * | 20 | (4,5) | 16.29 |
1 | x=[1 2 3 4 5 6 7 8 9 10] |
拟合效果
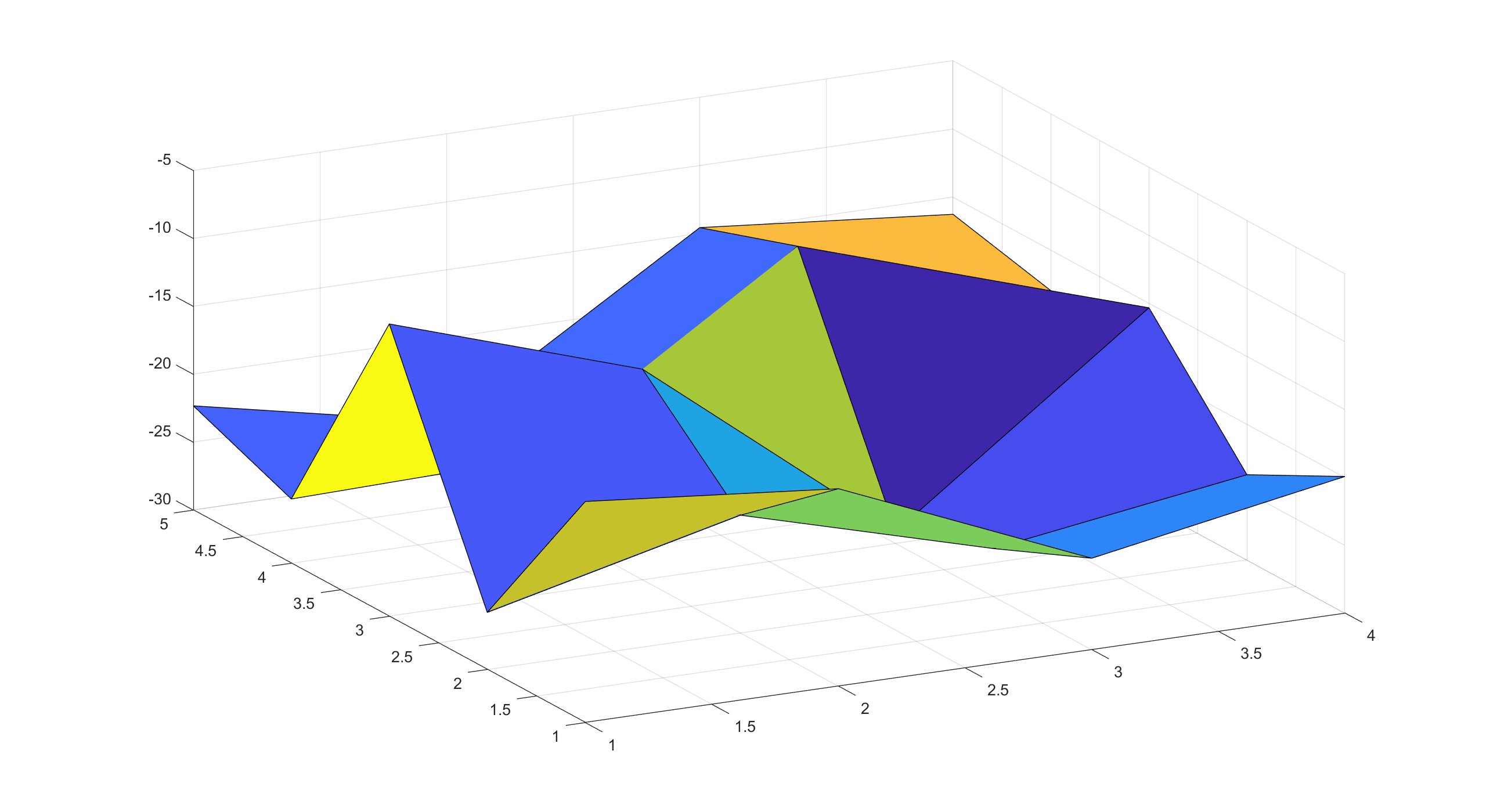
采用拟合的方法
1 |
|
出了问题,暂时搁置,以后解决!!
在客观世界中普遍存在着变量之间的关系,像某个现象的发生或某种结果的得出,往往与其他某个或某些因素有关,但这种关系又不是很确定的,只是从数据上可以看出“有关”的趋势。回归分析就是用来研究区域,有这种特征的变量之间的线性关系,用一定的线性回归模拟来你和因变量和自变量的数据,并通过确定模型参数得到回归方程.
7.1一元线性回归
当线性回归中的自变量只有一个时,称为一元线性回归假设,对于x(在某个区间内)的每一个值有:
其中, $a、b、\sigma^2$ 都是不依赖于 $x$ 的未知参数。记对于做这样的正态假设相当于假设
其中,未知参数都不依赖 $x$。
通常采用最小二乘法来确定。上面两个待定参数 $a$ 和 $b$ 及要求观测值与利用上面回归模型得到的拟合值之间的差值的平方和最小。差值平方和达到最小时的模型参数便作为待定参数的最终值,代入模型,即可得到回归方程。
在Matlab中,提供了polyfit函数来实现从一次到高次多项式的回归法。polyfit函数在前面章节已经介绍过,在此不再介绍。
1 | %% 输入数据 |
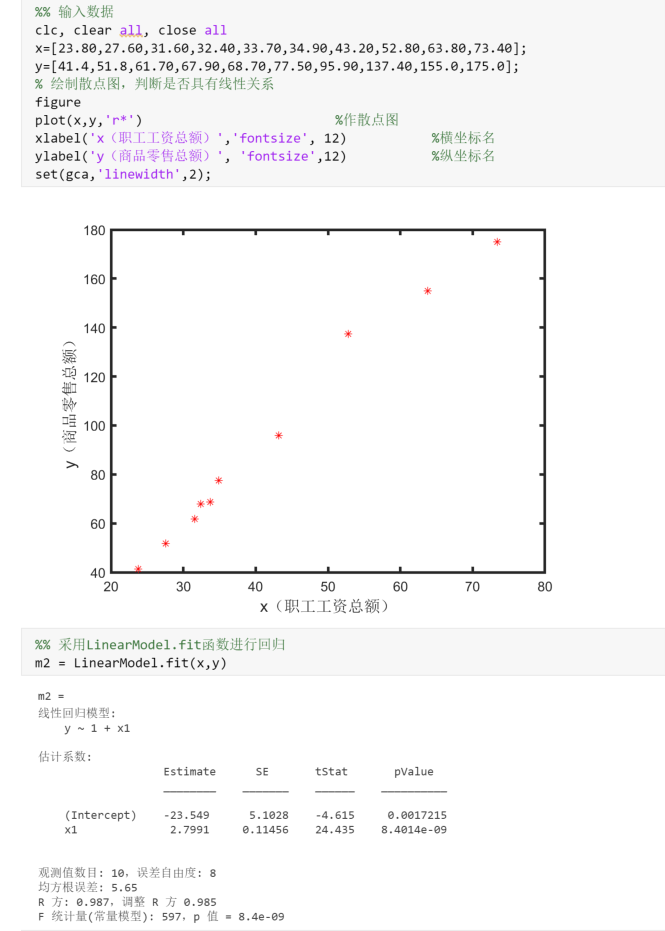
- 采用LinearModel.fit函数进行回归
- $[b, bint, r, rint, s] = regress(Y, X)$函数用于另外一种回归!
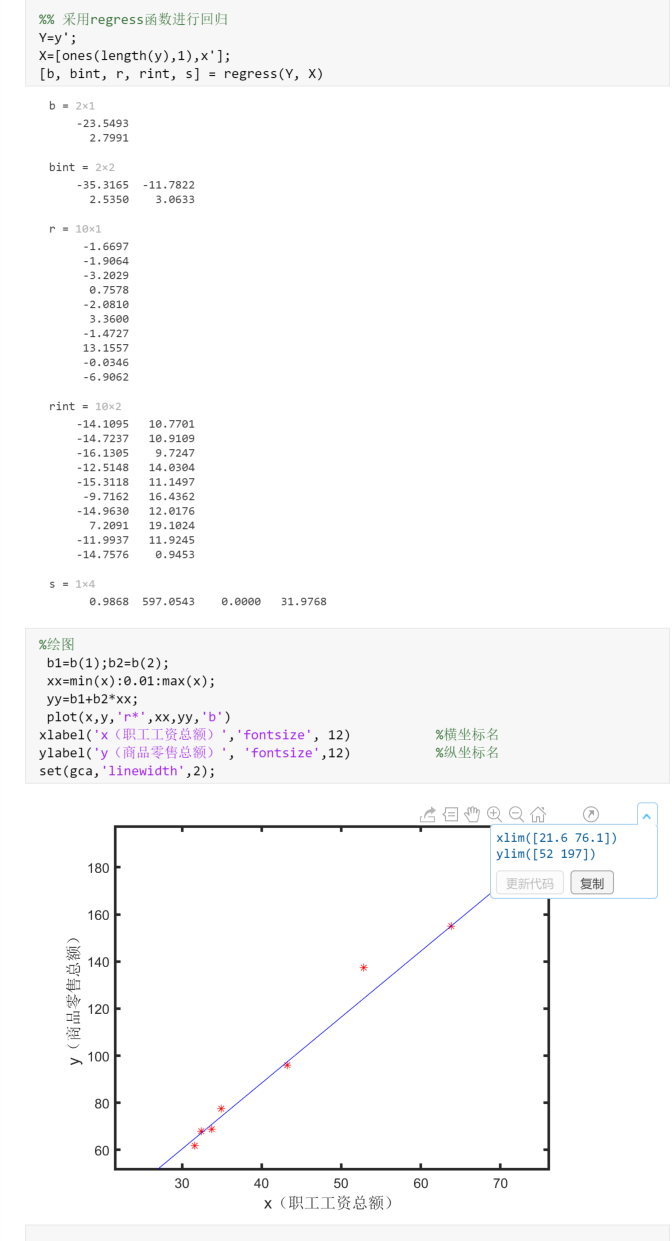
非线性回归
1 | %用nlinfit或fitnlm |
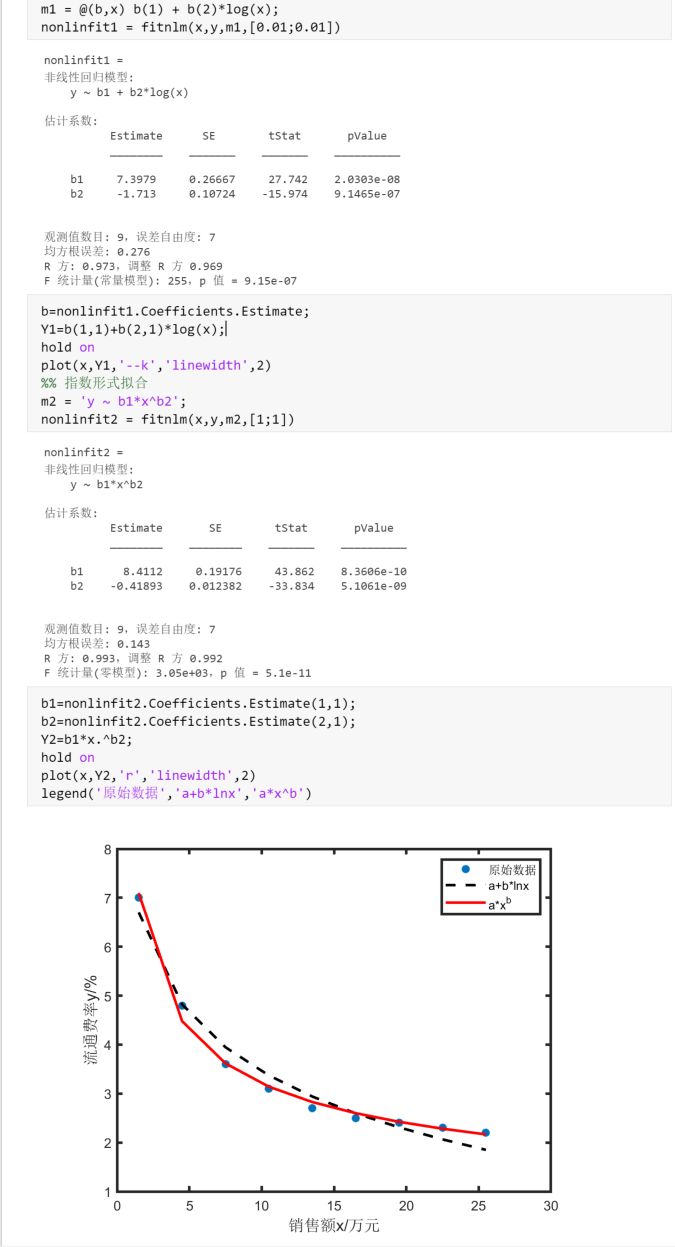
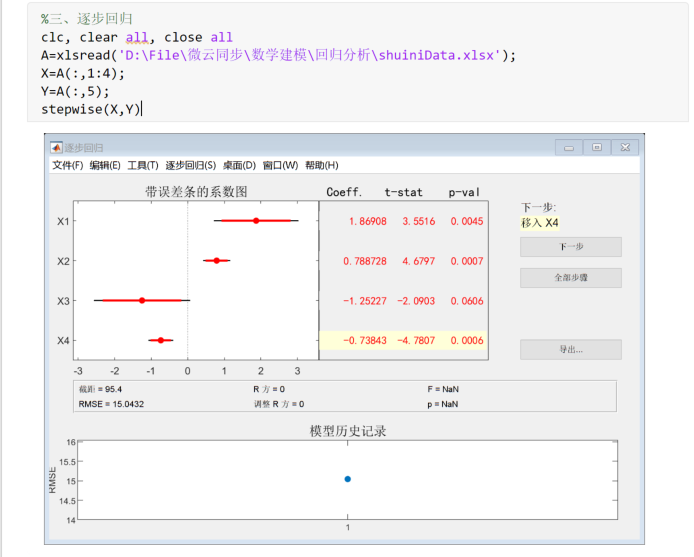
逐步回归